चित्र:DiffusionMicroMacro.gif
testwiki से
नेविगेशन पर जाएँ
खोज पर जाएँ
DiffusionMicroMacro.gif (३६० × ३०० चित्रतत्व, संचिका का आकार: ४०२ KB, माइम प्रकार: image/gif, चक्रित, ६० ढाँचे, ६.५ s)
यह चित्र विकिमीडिया कॉमन्स से है और दूसरे परियोजनाओं द्वारा भी प्रयोग की जा सकती है। वहाँ पर इसके चित्र विवरण पृष्ठ में मौजूद विवरण नीचे दिखाई गई है।
सारांश
| विवरणDiffusionMicroMacro.gif |
English: Diffusion from a microscopic and macroscopic point of view. Initially, there are solute molecules on the left side of a barrier (magenta line) and none on the right. The barrier is removed, and the solute diffuses to fill the whole container. Top: A single molecule moves around randomly. Middle: With more molecules, there is a clear trend where the solute fills the container more and more evenly. Bottom: With an enormous number of solute molecules, the randomness is gone: The solute appears to move smoothly and systematically from high-concentration areas to low-concentration areas, following Fick's laws.
Image is made in Mathematica, source code below. |
| दिनांक | |
| स्रोत | अपना कार्य |
| लेखक | Sbyrnes321 |
लाइसेंस
| Public domainPublic domainfalsefalse |
| मैं, इस कार्य का/की कॉपीराइट धारक, इस कार्य को सार्वजनिक डोमेन में प्रकाशित करता/करती हूँ। यह पूरे विश्व में लागू होता है। कुछ देशों में यह कानूनी तौर पर नहीं हो सकता है; ऐसा हो तो: मैं सभी को इस कार्य का इस्तेमाल किसी भी उद्देश्य से, बिना किसी बाधाओं के इन शर्तों के कानून द्वारा अनिवार्य किए तक करने की अनुमति देता/देती हूँ। |
<< Mathematica source code >>
(* Source code written in Mathematica 6.0, by Steve Byrnes, 2010.
I release this code into the public domain. Sorry it's messy...email me any questions. *)
(*Particle simulation*)
SeedRandom[1];
NumParticles = 70;
xMax = 0.7;
yMax = 0.2;
xStartMax = 0.5;
StepDist = 0.04;
InitParticleCoordinates = Table[{RandomReal[{0, xStartMax}], RandomReal[{0, yMax}]}, {i, 1, NumParticles}];
StayInBoxX[x_] := If[x < 0, -x, If[x > xMax, 2 xMax - x, x]];
StayInBoxY[y_] := If[y < 0, -y, If[y > yMax, 2 yMax - y, y]];
StayInBoxXY[xy_] := {StayInBoxX[xy[[1]]], StayInBoxY[xy[[2]]]};
StayInBarX[x_] := If[x < 0, -x, If[x > xStartMax, 2 xStartMax - x, x]];
StayInBarY[y_] := If[y < 0, -y, If[y > yMax, 2 yMax - y, y]];
StayInBarXY[xy_] := {StayInBarX[xy[[1]]], StayInBarY[xy[[2]]]};
MoveAStep[xy_] := StayInBoxXY[xy + {RandomReal[{-StepDist, StepDist}], RandomReal[{-StepDist, StepDist}]}];
MoveAStepBar[xy_] := StayInBarXY[xy + {RandomReal[{-StepDist, StepDist}], RandomReal[{-StepDist, StepDist}]}];
NextParticleCoordinates[ParticleCoords_] := MoveAStep /@ ParticleCoords;
NextParticleCoordinatesBar[ParticleCoords_] := MoveAStepBar /@ ParticleCoords;
NumFramesBarrier = 10;
NumFramesNoBarrier = 50;
NumFrames = NumFramesBarrier + NumFramesNoBarrier;
ParticleCoordinatesTable = Table[0, {i, 1, NumFrames}];
ParticleCoordinatesTable[[1]] = InitParticleCoordinates;
For[i = 2, i <= NumFrames, i++,
If[i <= NumFramesBarrier,
ParticleCoordinatesTable[[i]] = NextParticleCoordinatesBar[ParticleCoordinatesTable[[i - 1]]],
ParticleCoordinatesTable[[i]] = NextParticleCoordinates[ParticleCoordinatesTable[[i - 1]]]];];
(*Plot full particle simulation*)
makeplotbar[ParticleCoord_] :=
ListPlot[{ParticleCoord, {{xStartMax, 0}, {xStartMax, yMax}}}, Frame -> True, Axes -> False,
PlotRange -> {{0, xMax}, {0, yMax}}, Joined -> {False, True}, PlotStyle -> {PointSize[.03], Thick},
AspectRatio -> yMax/xMax, FrameTicks -> None];
makeplot[ParticleCoord_] :=
ListPlot[ParticleCoord, Frame -> True, Axes -> False, PlotRange -> {{0, xMax}, {0, yMax}}, Joined -> False,
PlotStyle -> PointSize[.03], AspectRatio -> yMax/xMax, FrameTicks -> None]
ParticlesPlots =
Join[Table[makeplotbar[ParticleCoordinatesTable[[i]]], {i, 1, NumFramesBarrier}],
Table[makeplot[ParticleCoordinatesTable[[i]]], {i, NumFramesBarrier + 1, NumFrames}]];
(*Plot just the first particle in the list...Actually the fifth particle looks better. *)
FirstParticleTable = {#[[5]]} & /@ ParticleCoordinatesTable;
FirstParticlePlots =
Join[Table[makeplotbar[FirstParticleTable[[i]]], {i, 1, NumFramesBarrier}],
Table[makeplot[FirstParticleTable[[i]]], {i, NumFramesBarrier + 1, NumFrames}]];
(* Continuum solution *)
(* I can use the simple diffusion-on-an-infinite-line formula, as long as I correctly periodically replicate the
initial condition. Actually just computed nearest five replicas in each direction, that was a fine approximation. *)
(* k = diffusion coefficient, visually matched to simulation. *)
k = .0007;
u[x_, t_] := If[t == 0, If[x <= xStartMax, 1, 0], 1/2 Sum[
Erf[(x - (-xStartMax + 2 n xMax))/Sqrt[4 k t]] - Erf[(x - (xStartMax + 2 n xMax))/Sqrt[4 k t]], {n, -5, 5}]];
ContinuumPlots = Join[
Table[Show[
DensityPlot[1 - u[x, 0], {x, 0, xMax}, {y, 0, yMax},
ColorFunctionScaling -> False, AspectRatio -> yMax/xMax,
FrameTicks -> None],
ListPlot[{{xStartMax, 0}, {xStartMax, yMax}}, Joined -> True,
PlotStyle -> {Thick, Purple}]],
{i, 1, NumFramesBarrier}],
Table[
DensityPlot[1 - u[x, tt], {x, 0, xMax}, {y, 0, yMax},
ColorFunctionScaling -> False, AspectRatio -> yMax/xMax,
FrameTicks -> None],
{tt, 1, NumFramesNoBarrier}]];
(*Combine and export *)
TogetherPlots =
Table[GraphicsGrid[{{FirstParticlePlots[[i]]}, {ParticlesPlots[[i]]}, {ContinuumPlots[[i]]}},
Spacings -> Scaled[0.2]], {i, 1, NumFrames}];
Export["test.gif", Join[TogetherPlots, Table[Graphics[], {i, 1, 5}]],
"DisplayDurations" -> {10}, "AnimationRepititions" -> Infinity ]
Captions
Add a one-line explanation of what this file represents
ব্যাপন প্রক্রিয়া
Items portrayed in this file
चित्रण
some value
source of file अंग्रेज़ी
original creation by uploader अंग्रेज़ी
१६ जनवरी 2010
media type अंग्रेज़ी
image/gif
चित्र का इतिहास
चित्र पुराने समय में कैसी दिखती थी यह जानने के लिए दिनांक/समय पर क्लिक करें।
| दिनांक/समय | थंबनेल | आकार | सदस्य | टिप्पणी | |
|---|---|---|---|---|---|
| वर्तमान | १४:४१, ७ मार्च २०१२ | 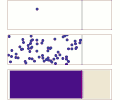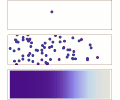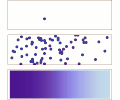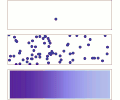 | ३६० × ३०० (४०२ KB) | wikimediacommons>Dratini0 | Just removed the white last fram for aesthetic purposes, and prologed the display time of the last frame to mark the reatart of the animation. |
चित्र का उपयोग
यह पृष्ठ इस चित्र का इस्तेमाल करता है:


