चित्र:Piecewise linear function2D.svg
testwiki से
नेविगेशन पर जाएँ
खोज पर जाएँ

पूर्वावलोकन PNG का आकार SVG फ़ाइल: ४४३ × ४४३ पिक्सेल दूसरे रेसोल्यूशन्स: २४० × २४० पिक्सेल | ४८० × ४८० पिक्सेल | ७६८ × ७६८ पिक्सेल | १,०२४ × १,०२४ पिक्सेल | २,०४८ × २,०४८ पिक्सेल।
मूल चित्र (SVG फ़ाइल, साधारणतः ४४३ × ४४३ पिक्सेल, फ़ाइल का आकार: ६० KB)
यह चित्र विकिमीडिया कॉमन्स से है और दूसरे परियोजनाओं द्वारा भी प्रयोग की जा सकती है। वहाँ पर इसके चित्र विवरण पृष्ठ में मौजूद विवरण नीचे दिखाई गई है।
सारांश
| विवरणPiecewise linear function2D.svg | Illustration of a piecewise linear function |
| दिनांक | |
| स्रोत | अपना कार्य |
| लेखक | Oleg Alexandrov |
| SVG genesis InfoField |
लाइसेंस
| Public domainPublic domainfalsefalse |
| इस कार्य को इसके लेखक, Oleg Alexandrov द्वारा सार्वजनिक डोमेन में प्रकाशित किया गया है। यह पूरे विश्व में लागू होता है। कुछ देशों में यह कानूनी तौर पर नहीं हो सकता है; ऐसा हो तो: Oleg Alexandrov सभी को इस कार्य का इस्तेमाल किसी भी उद्देश्य से, बिना किसी बाधाओं के इन शर्तों के कानून द्वारा अनिवार्य किए तक करने की अनुमति देता/देती हैं। |
Source code (MATLAB)
% Draw a piewise-linear function in two dimensions on a given triangulation.
% Due to a bug in plot2svg, it can't export 3D pictures well.
% Then, I have to take the 3D picture, and rotate and project it manually to 2D.
% That makes the code more complicated.
function main()
% read the triangulation from the data at the end of the code
dummy_arg = 0;
node=get_nodes(dummy_arg); [np, k]=size(node);
ele=get_triangles(dummy_arg); [nt, k]=size(ele);
% the function whose piecewise-linear approximation will be graphed
f=inline('0.07*(22-8*x^2-10*y^2)+0.14');
% will keep here the triangles to plot and their colors
P = zeros(3*nt, 3);
C = zeros(nt, 3);
% iterate through triangles, save the coordinates of all the triangles
alpha=0.3;
for i=1:nt;
u=ele(i,2); v=ele(i, 3); w=ele(i, 4);
y1=node(u, 2); x1=node(u, 3); f1=f(x1, y1);
y2=node(v, 2); x2=node(v, 3); f2=f(x2, y2);
y3=node(w, 2); x3=node(w, 3); f3=f(x3, y3);
% the color of the given triangle is chosen randomly
color = alpha*rand(1, 3)+(1-alpha)*[1 1 1];
% store the triangle and its color for the future
m = 3*i - 2;
P(m+0, 1) = x1; P(m+0, 2) = y1; P(m+0, 3) = f1;
P(m+1, 1) = x2; P(m+1, 2) = y2; P(m+1, 3) = f2;
P(m+2, 1) = x3; P(m+2, 2) = y3; P(m+2, 3) = f3;
C(i, :) = color;
end
% the "base", the domain of the piecewise linear function
P0 = P; P0(:, 3) = 0*P0(:, 3);
% Do a rotation in 3D, then plot the projections onto the xy-plane.
% This has to be done by hand since plot2svg has trouble saving 3D graphics
a = pi/2.5; b = 0; c = 0;
Q = do_rotate(P, a, b, c);
Q0 = do_rotate(P0, a, b, c);
% sort the triangles by the third coordinate of the center of gravity (after the rotation)
R = zeros(nt, 2);
for i=1:nt
m = 3*i-2;
z1=Q(m, 3);
z2=Q(m+1, 3);
z3=Q(m+2, 3);
R(i, 1) = (z1+z2+z3)/3;
R(i, 2) = i;
end
R = sortrows(R, 1);
% plot the projection of the rotated figure and the base shape
clf; hold on; axis equal; axis off;
lw = 0.5; black = [0, 0, 0]; white = [1, 1, 1];
for i = 1:nt
j = R(i, 2);
m = 3*j-2;
fill([Q(m, 1), Q(m+1, 1) Q(m+2, 1)], [Q(m, 2), Q(m+1, 2) Q(m+2, 2)], C(i, :));
fill([Q0(m, 1), Q0(m+1, 1) Q0(m+2, 1)], [Q0(m, 2), Q0(m+1, 2) Q0(m+2, 2)], white);
plot([Q(m, 1), Q(m+1, 1) Q(m+2, 1), Q(m, 1)], [Q(m, 2), Q(m+1, 2) Q(m+2, 2), Q(m, 2)], ...
'linewidth', lw, 'color', black);
plot([Q0(m, 1), Q0(m+1, 1) Q0(m+2, 1), Q0(m, 1)], [Q0(m, 2), Q0(m+1, 2) Q0(m+2, 2), Q0(m, 2)], ...
'linewidth', lw, 'color', black);
end
% a small fix to avoid a bug with the bounding box when exporting
small = 0.1;
Sx = min(min(Q(:, 1)), min(Q0(:, 1)))-small; Lx = max(max(Q(:, 1)), max(Q0(:, 1)))+small;
Sy = min(min(Q(:, 2)), min(Q0(:, 2)))-small; Ly = max(max(Q(:, 2)), max(Q0(:, 2)))+small;
plot(Lx, Ly, '*', 'color', 0.99*white);
plot(Sx, Sy, '*', 'color', 0.99*white);
axis([Sx-small Lx+small, Sy-small, Ly+small])
% export as eps and svg
% saveas(gcf, 'piecewise_linear2D_proj.eps', 'psc2')
plot2svg('piecewise_linear2D_proj.svg')
function node = get_nodes (dummy_arg)
node =[1 1 0
2 0.913545 0.406737
3 0.669131 0.743145
4 0.309017 0.951057
5 -0.104528 0.994522
6 -0.5 0.866025
7 -0.809017 0.587785
8 -0.978148 0.207912
9 -0.978148 -0.207912
10 -0.809017 -0.587785
11 -0.5 -0.866025
12 -0.104528 -0.994522
13 0.309017 -0.951057
14 0.669131 -0.743145
15 0.913545 -0.406737
16 -0.161265 -0.179103
17 0.313878 0.228046
18 -0.314083 0.348825
19 0.40037 -0.290886
20 0.0609951 -0.58033
21 0.0617879 0.587873
22 -0.587046 1.34875e-16];
function ele = get_triangles(dummy_arg)
ele=[1 10 11 16
2 16 18 22
3 10 22 9
4 10 16 22
5 11 12 20
6 7 22 18
7 21 3 4
8 8 9 22
9 8 22 7
10 1 19 15
11 20 13 14
12 6 18 21
13 6 21 5
14 19 1 17
15 19 16 20
16 11 20 16
17 2 17 1
18 16 17 18
19 6 7 18
20 17 16 19
21 21 4 5
22 3 17 2
23 17 3 21
24 20 12 13
25 19 20 14
26 18 17 21
27 14 15 19];
function Q = do_rotate(P, a, b, c)
M = [1, 0, 0; 0, cos(a), sin(a); 0 -sin(a), cos(a)]*[cos(b), 0, -sin(b); 0, 1, 0; sin(b), 0, cos(b)]...
*[cos(c), sin(c), 0; -sin(c), cos(c), 0; 0, 0, 1];
[m, n] = size(P);
Q = 0*P;
for i=1:m
X = P(i, :)';
X = M*X;
Q(i, 1) = X(1);
Q(i, 2) = X(2);
Q(i, 3) = X(3);
end
Captions
Add a one-line explanation of what this file represents
Piecewise linear function
Items portrayed in this file
चित्रण
some value
data size अंग्रेज़ी
६१,५७४ बाइट
media type अंग्रेज़ी
image/svg+xml
checksum अंग्रेज़ी
09a37c8a446c97777a6d2707fcd3f116d79bb591
चित्र का इतिहास
चित्र पुराने समय में कैसी दिखती थी यह जानने के लिए दिनांक/समय पर क्लिक करें।
| दिनांक/समय | थंबनेल | आकार | सदस्य | टिप्पणी | |
|---|---|---|---|---|---|
| वर्तमान | ०१:१३, १८ जुलाई २००७ | 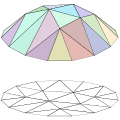 | ४४३ × ४४३ (६० KB) | wikimediacommons>Oleg Alexandrov | tweak |
चित्र का उपयोग
यह पृष्ठ इस चित्र का इस्तेमाल करता है: