लोलक

"सरल गुरुत्वीय लोलक" शून्य वायु-घर्षण एवं प्रतिरोध मानकर

किसी खूंटी से लटके ऐसे भार को लोलक (साँचा:Lang-la) कहते हैं जो स्वतंत्रतापूर्वक आगे-पीछे झूल सकता हो। झूला इसका एक व्यावहारिक उदाहरण है।

आवर्त काल (Period of oscillation)

लोलक का एनिमेशन - इसमें लोलक की परिवर्तनशील वेग एवं त्वरण सदिशों को दर्शाया गया है। (v एवं A).

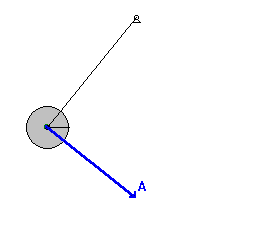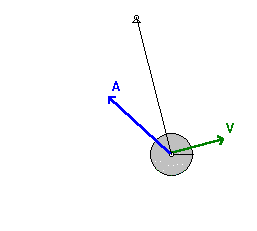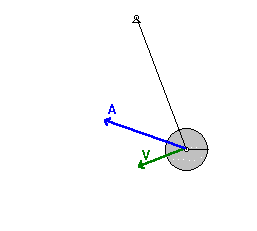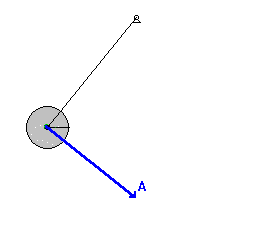
साँचा:PhysicsNavigation दोलन करता हुआ लोलक किसी एक बिन्दु जितने समय बाद पुनः वापस आ जाता है उसे उसका 'आवर्तकाल' कहते हैं। यदि लोलक का आयाम कम हो तो इसका आवर्तकाल आयाम पर निर्भर नहीं करता बल्कि केवल लोलक की लम्बाई और गुरुत्वजनित त्वरण के स्थानीय मान पर निर्भर होता है। लोलक का आवर्तकाल लोलक के द्रव्यमान पर भी निर्भर नहीं करता।

$T\approx 2\pi \sqrt{\frac{L}{g}}{\theta }_0\ll 1(1)$

जहाँ L लोलक की लम्बाई है, तथा g उस स्थान पर गुरुत्वजनित त्वरण का मान है।

इस सूत्र से साफ है कि यदि आयाम (या स्विंग) कम हो तो आवर्तकाल अलग-अलग आयामों के लिये समान होगा। लोलक के इस गुण को 'समकालिकता' (isochronism) कहते हैं। अपने इसी गुण के कारण लोलक का उपयोग समयमापन (timekeeping) में खूब हुआ।

किन्तु यदि आयाम बड़ा है तो आवर्तकाल नियत नहीं रहता बल्कि आयाम बढ़ने पर क्रमशः बढ़ता है। उदाहरण के लिये यदि आयाम θ₀ = 23° हो तो आवर्तकाल का मान समीकरण (1) से प्राप्त मान से लगभग १% अधिक होगा।

लोलक के किसी भी आयाम (छोटे या बड़े) के लिये आवर्तकाल का मान निम्नलिखित अनन्त श्रेणी द्वारा दी जाती है-

$\begin{array}{cc}T& =2\pi \sqrt{\frac{L}{g}}(1+\frac{1}{16}{\theta }_0^2+\frac{11}{3072}{\theta }_0^4+\frac{173}{737280}{\theta }_0^6+\frac{22931}{1321205760}{\theta }_0^8+\cdots )\end{array}$

एक फ्रांसीसी घड़ी में लगा अलंकारिक लोलक

विभिन्न प्रकार

• सरल लोलक
• द्विक लोलक
• असरल लोलक या पिण्ड लोलक (कम्पाउण्ड पेण्डुलम)
• चुम्बकीय लोलक
• सैकेन्डी लोलक
• बैलिस्टिक लोलक
• फूको का लोलक (Foucault pendulum)
• न्यूटन का लोलक
• विमोटन लोलक (टॉर्शन पेंडुलम)

इन्हें भी देखें

• लोलक घड़ी
• लोलक (गणित)
• सरल आवर्त गति